一阶带通滤波器电路图原理
分析和测试的方法。测试根据结果得出,使用该方法设计的带通滤波器具有稳定性很高。设计难度小等优点,也为滤波器的设计提供了一个新的思路。
带通滤波器是一种仅允许特定频率通过,同时对其余频率的信号进行相对有效抑制的电路。由于它对信号具有选择性,故而被广泛地应用现在电子设计中。但是,带通滤波器的种类非常之多,各个类型的设计差异也很大,这就导致了在传统滤波器的设计方法中不可避免地要进行大量的理论计算与分析,不但损失了宝贵的时间,同时也提升了电路的设计门槛。未解决上述弊端,下面介绍了一种使用FilterPro和Proteus相结合的有源带通滤波器的设计的具体方案,随着EDA技术的持续不断的发展,这种方法的优势也将越来越明显。
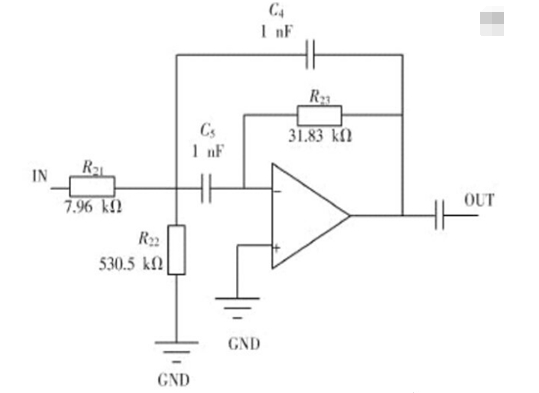
电路原理图如图1所示。然后可在Proteus中搭建电路进行仿真分析,前面已经提到,FilterPro生成的滤波器中的运放使用的理想运放模型,所以仿真时需要先用理想运放做多元化的分析,然后再进行替换。
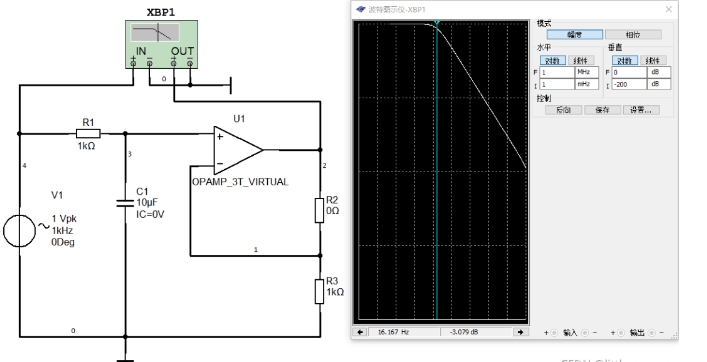
图2中,R1和C1构成了无源的RC低通滤波器,运放只起到跟随或放大的作用。
通过选择R2和R3的值可以将输出信号放大,这里仿线仅仅是为了不放大,便于观察波特图。
下面讨论设计两种带通滤波器,其一为二阶低通滤波器和二阶高通滤波器组成的四阶带通滤波器,如下图:
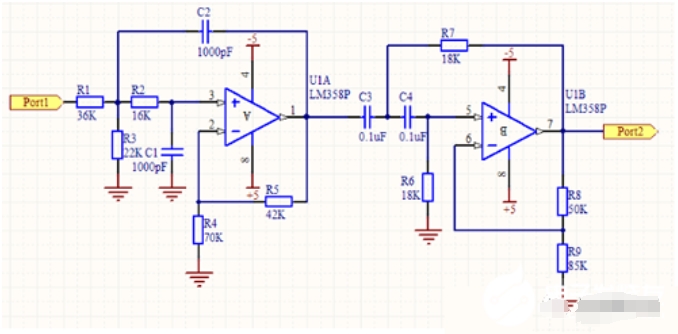
对于低通滤波器的设计,电容一般选取1000pF,对于高通滤波器的设计,电容一般选取0.1uF,然后根据公式R=1/2Πfc计算得出与电容相组合的电阻值,即得到此图中R2、R6和R7,为了消除运放的失调电流造成的误差,尽量是运放同相输入端与反向输入端对地的直流电阻基本相等,同时巴特沃斯滤波器阶数与增益有一定的关系(见表1),根据这两个条件可以列出两个等式:30=R4*R5/(R4 R5),R5=R4(A-1),36=R8*R9/(R8 R9),R8=R9(A-1)由此能够解出R4、R5、R8、R9,原则是根据现实情况稍调整电阻值保持在一定限度内即可,不要相差太大,注意频率别超过运放的标定频率。
本文粗略地介绍一阶带通滤波器电路图的原理,虽然,它们一般只是由无源器件R、C在起作用,电路中的运放只是跟随或者放大信号,但是加入运放后,它具有不少优点。
由于运放的输入阻抗极高,使得RC滤波电路的输出端不会受到负载的影响(等同于RC电路后端不接负载的情况);另外运放的能够更好的起到信号放大,增强驱动能力的作用。
但是由于运放的带宽有限,会使得有源滤波器的有效带宽范围只能在运放的带宽范围内,不能够做到极高的频段。






 时间: 2024-03-02
时间: 2024-03-02  作者:
作者: 

