，这一层在神经网络中有啥作业，以及它和矩阵乘法、卷积运算有啥联络呢？

  之所以这么叫，是因为这一层的每个神经元都与前一层的每个神经元衔接在一起，构成了一个全衔接的网络结构。

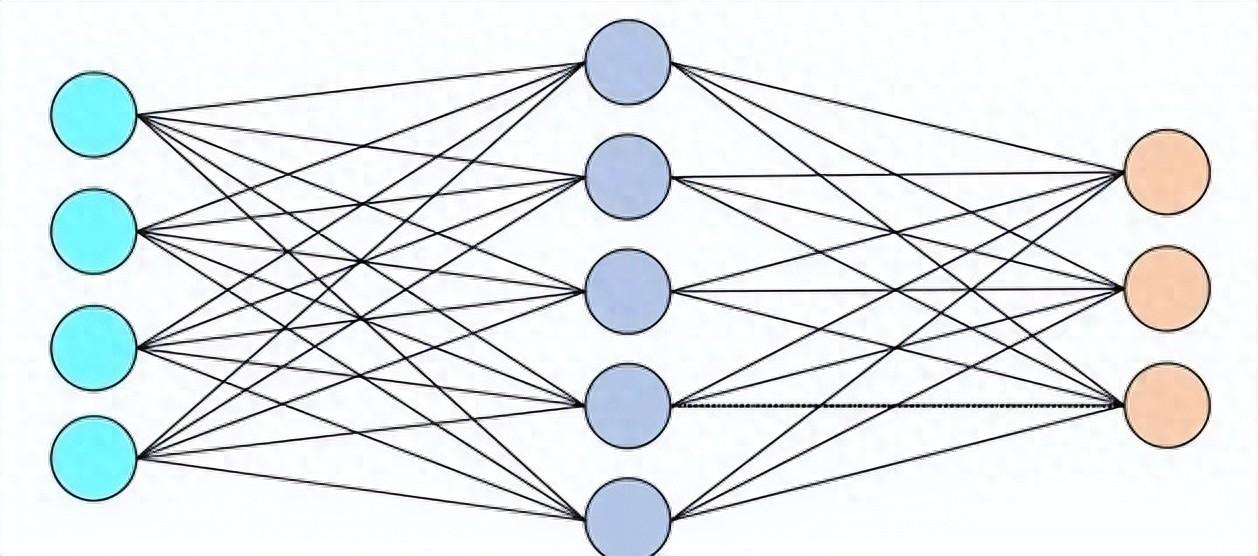
  这种全衔接的方法与卷积和池化不同，卷积和池化是经过固定巨细的卷积核或池化窗口在输入上移动，以便有用地捕捉部分特征。

  因而，全衔接强调了这一层中的神经元与前一层中的一切神经元之间的衔接，与卷积和池化层的部分衔接方法构成比照。

  既然是一切神经元的悉数衔接，阐明它能够捕获到前面一切的特征，经过运算就能愈加有用、齐备的交融一切特征。

  使得神经网络终究看到的特征是个大局特征（一只猫），而不是部分特征（眼睛或许鼻子）。

  假定你是一只蚂蚁，你的使命是找小面包。这时候你的视界比较窄，只能看到很小一片区域，也就只能看到一个大面包的部分。

  当你找到一片面包之后，你底子不知道你找到的是不是悉数的面包，所以你们一切的蚂蚁开了个会。

  你们相互把自己找到的面包的信息同享出来，经过开会同享，终究你们承认，哦，你们找到了一个大面包。

  上面说的蚂蚁开会的进程，便是全衔接，这也是为什么，全衔接需要把一切的节点都衔接起来，尽可能的完结一切节点的信息同享。

  单纯从数学运算上来看，全衔接便是矩阵运算，关于矩阵运算的实质，这儿说的更明晰一些：5分钟搞懂矩阵乘法的实质。

  全衔接和卷积的差异，除了上面说的前者是大局视界，卷积是部分视界之外，还有一个很重要的联络。

  那便是假如卷积的卷积核变为1x1，那么相当于卷积核的每一个像素都与输入图片的每一个像素相关联，此刻1x1的卷积，也就变成了矩阵乘了。

  假定神经网络前面很多层学到了1000个特征，那么最终一层全衔接就能够把这1000个特征进行悉数交融，交融之后就不难得知这张图片是一只狗。

  借用“图灵的猫”对这个算法的解说：全衔接层在整个卷积神经网络中起到“分类器”的效果。

  假如说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全衔接层则起到将学到的“分布式特征表明”映射到样本符号空间的效果。